Les opérations de mesure de grandeurs (longueur d'une courbe, aire, volume, flux...) et de calcul de probabilités étant souvent soumises à des calculs d'intégrales, l'intégration est un outil scientifique fondamentale. C'est la raison pour laquelle l'intégration est souvent abordée dès l'enseignement secondaire.
Les différents domaines dans lesquels peuvent se rencontrer des intégrales ont conduit à donner des définitions différentes de l'intégrale permettant d'en calculer pour des fonctions de moins en moins régulières. On rencontre ainsi les intégrales dites de Riemman, de Lebesgue ou de de Kurzweil-Henstock. Mais toutes ces définitions coïncident dans le cas des fonctions continues.
Le symbole mathématique représentant l'intégration,
, est appelé
signe somme,
signe d'intégration, signe intégral ou
intégrateur ; il a été introduit par Leibniz.
Dans un plan muni d'un repère cartésien, on choisit comme unité d'aire, l'aire du quadrilatère OIKJ où O est l'origine du repère et I, J et K les points de coordonnées respectives (1 ; 0), (0 ; 1) et (1 ; 1).
Si f est une fonction réelle positive continue prenant ses valeurs dans un segment I = [a, b], alors l'intégrale de f sur I, notée
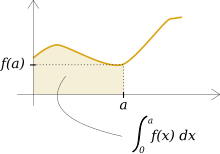
est l'aire d'une surface délimitée par la représentation graphique de f et par les trois droites d'équation x = a, x = b, y = 0, surface notée Sf. (Voir schéma ci-contre pour l'intervalle I = [0, a].)
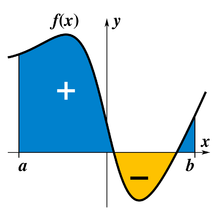On donne un signe positif à l'aire des surfaces comme Sf situées au-dessus de l'axe des abscisses. Pour pouvoir traiter aussi les fonctions négatives, on donne un signe négatif aux portions situées sous cet axe.
Ainsi, pour définir l'intégrale d'une fonction continue dans le cas général (positive ou négative), il suffit de définir f + et f –comme suit :
puis de définir l'intégrale de f à partir de f + et f –, fonctions continues et positives :
Plus précisément, définir l'aire de cette surface consiste, dans la définition de la théorie de Riemann, à approcher f par une suite de fonctions gn dont on connait l'intégrale (en général : des rectangles qu'on définit d'aire ± longueur × largeur) et telle que la différence entre f et gn tende vers 0 quand n tend vers l'infini.
Il se trouve qu'avec cette méthode, il est possible de définir l'aire d'une fonction continue bornée présentant un ensemble dénombrable de points de discontinuité.
On appelle f un intégrande, et on note ∫ (un s allongé, mis pour somme) l'opérateur mathématique, appelé intégrateur, qui est associé à l'intégration. Ce symbole est un ancien s long : en effet, Leibniz s'est servi de l'initiale du mot latin summa, « somme », lequel était le plus souvent écrit ſumma. À la différence du s long, ∫, en typographie, garde toujours une hampe descendant au-dessous de la ligne de base, en romaine comme en italique. Voir l'article Notation de Leibniz pour une justification de la notation complète, et en particulier du symbole dx.
